Вынос пикета на кривую
Положим, что начало кривой имеет пикетажное наименование ПК(НК) = ПКN + s1. При радиусе закругления R по формулам (1.24), (1.25) находим
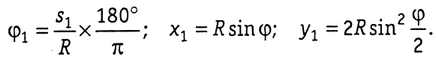
Отложив значения x1, у2, находим положение ПКN + s1на кривой.
Способ углов, или полярный способ, заключается в том, что из точки А (рис. 1.34) на окружности через равные дуги s между касательной и секущей имеем углы, равные половине центрального угла φ.
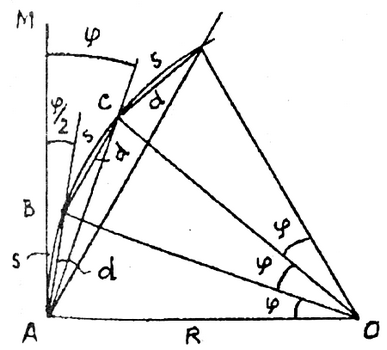
Рис. 1.34. Способ углов
На рисунке 1.34 хорда
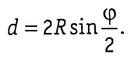
откуда
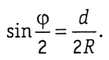(1.26.)
Установив в точке А теодолит, совмещают нулем лимба с нулем алидады, визируют на точку М и от направления AM вращением алидады откладывают угол φ / 2. Отложив по направлению визирного луча отрезок d, получают точку В кривой. Затем вращением алидады откладывают угол φ. Совместив начало ленты (рулетки) с точкой 5 и отложив на ленте отрезок d, поворачивают ее до совпадения конца отрезка d с визирным лучом и получают точку С и т. д. Недостаток способа — рост ошибок по мере увеличения числа точек на кривой. Способ используют при разбивке кривых на насыпи или выемке и когда способ координат неудобен.
Способ продолженных хорд (рис. 1.35). Точку В на кривой определяют линейной засечкой из точек А и В', откладывая из точки А лентой хорду d и рулеткой из точки В' отрезок у. Точку В' определяют путем откладывания по оси абсцисс хорды d. По направлению АВ (продолжение хорды) откладывают хорду d и получают точку С'. Отложив от точки В хорду d и от С' отрезок к линейной засечкой получают точку С и т. д. Из подобных треугольников ОВС и ВС'С имеем
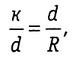
откуда
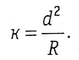
Так как в треугольнике АВ'В угол В'АВ равен φ/2, то можно считать у = к/2 Этот способ применяют в местах, где нельзя использовать метод прямоугольных координат. Следует заметить, что первую точку В на кривой можно определить методом прямоугольных координат, для чего нужно знать угоде который можно определить по формуле (1.26).
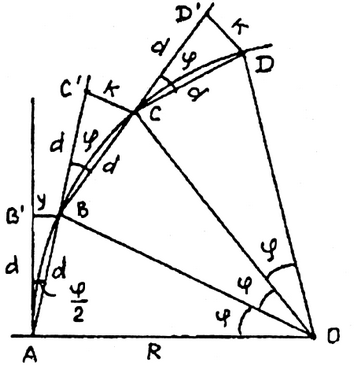
Рис. 1.35. Способ продолженных хорд
